高中数学必备图象有哪些?
在高中数学学习过程中,掌握核心函数图象是理解代数与几何联系的关键,函数图象能够直观展现变量之间的关系,帮助学习者建立数形结合的思维方式,以下是高中数学课程中需要重点掌握的几类函数图象及其特征。
一次函数图象一次函数表达式为y=kx+b,其图象为一条直线,斜率k决定直线的倾斜程度与方向,当k>0时直线呈上升趋势,k<0时呈下降趋势,纵截距b表示直线与y轴交点的位置,通过改变k与b的数值,可以观察到直线在坐标系中的平移与旋转现象。
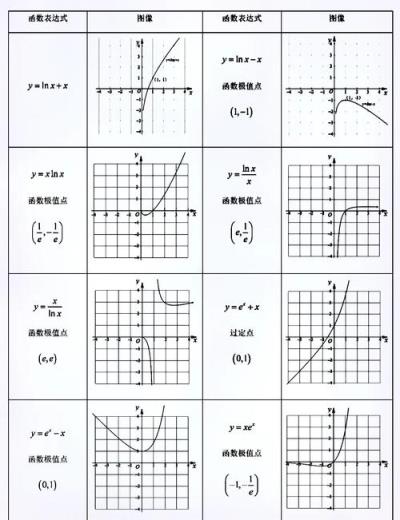
二次函数图象二次函数的一般形式为y=ax²+bx+c,图象呈现抛物线形态,系数a的正负决定抛物线开口方向,a>0时开口向上,a<0时开口向下,顶点坐标为函数的最值点,对称轴为通过顶点且垂直于x轴的直线,通过配方法可将一般式转化为顶点式,更直观地读取图象特征。
指数函数图象指数函数表达式为y=a^x(a>0且a≠1),图象恒过点(0,1),当底数a>1时,函数呈现快速增长趋势;当0 对数函数图象对数函数的一般形式为y=log_a x(a>0且a≠1),图象恒过点(1,0),当底数a>1时,函数缓慢递增;当0 三角函数图象正弦函数y=sin x与余弦函数y=cos x的图象呈现周期性波动特征,正弦曲线通过原点,余弦曲线在y轴上的截距为1,这两种函数的振幅、周期和相位变化都会影响波形特征,正切函数y=tan x图象由无数个间断的曲线段组成,在每个周期内从负无穷增至正无穷。 幂函数图象幂函数表达式为y=x^a,其图象形态随指数a的变化呈现显著差异,当a为正整数时,图象通过原点且在第一象限单调递增;当a为负整数时,图象分为两支且以坐标轴为渐近线;当a为分数时,图象可能仅存在于部分象限,理解幂函数图象需要结合指数运算的基本性质。 掌握这些函数图象不仅有助于解决数学问题,更能培养空间想象能力,在学习过程中,建议通过描点法亲手绘制函数图象,观察参数变化对图形的影响,函数图象是数学语言的重要组成部分,熟练运用这种工具将使数学问题的分析过程更加直观高效。 本站通过AI自动登载优质内容,本文来源于互联网或者用户投稿,本站旨在传播优质文章,无商业用途。如不想在本站展示可联系删除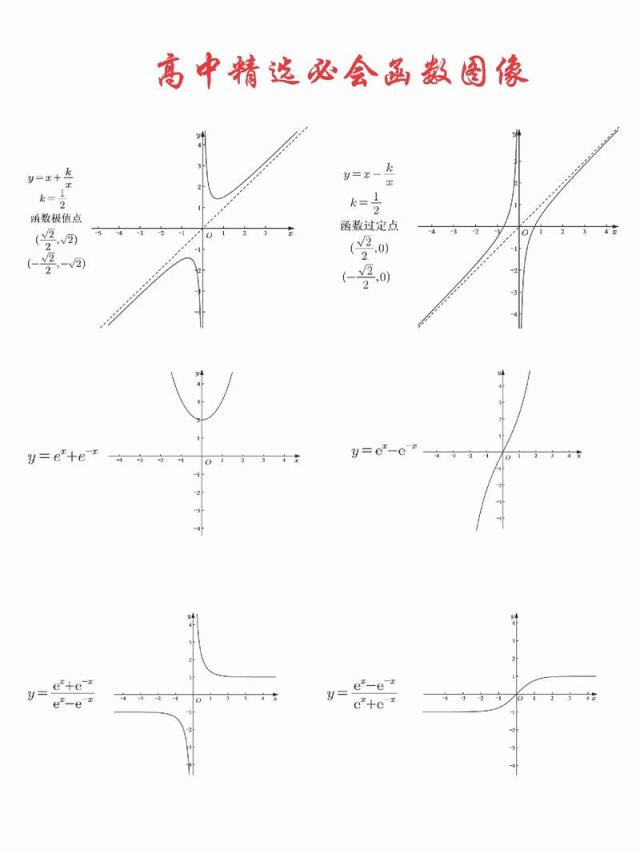
本站部分文章来自网络或用户投稿。涉及到的言论观点不代表本站立场。阅读前请查看【免责声明】发布者:爱自由,如若本篇文章侵犯了原著者的合法权益,可联系我们进行处理。本文链接:https://www.sxhanhai.com/xkzl/shuxue/139505.html
上一篇:高中数学有哪些图型题?
下一篇:高中数学辅助教具有哪些?




