高中数学有哪些图型题？

高中数学的图形题主要分布在几个核心板块，这些题目不仅考察对图形性质的理解,也考验数形结合的解题能力。

函数图像相关问题是高中数学的重中之重，核心在于掌握基本初等函数的图像,并能通过函数性质分析图像变化。

1. 基本函数识别与性质分析：要求能够快速画出一次函数、二次函数、指数函数、对数函数、幂函数以及三角函数（正弦、余弦、正切）的图像，题目常考察函数的定义域、值域、单调性、奇偶性、周期性等。

2. 函数图像变换：这是高频考点，需要熟练掌握图像的平移变换（左加右减，上加下减）、对称变换（关于x轴、y轴、原点）、伸缩变换（横向、纵向）规律，给出函数f(x)的图像，要求画出f(2x+1)的图像。

   

3. 数形结合求参数范围：题目常给出一个含参数的方程或不等式，通过将其转化为两个函数图像的交点问题或上下位置关系，来求解参数的取值范围，讨论方程 |x| = kx + 1 的实数根个数。

平面几何与立体几何图形题

几何部分对空间想象能力和逻辑推理能力要求较高。

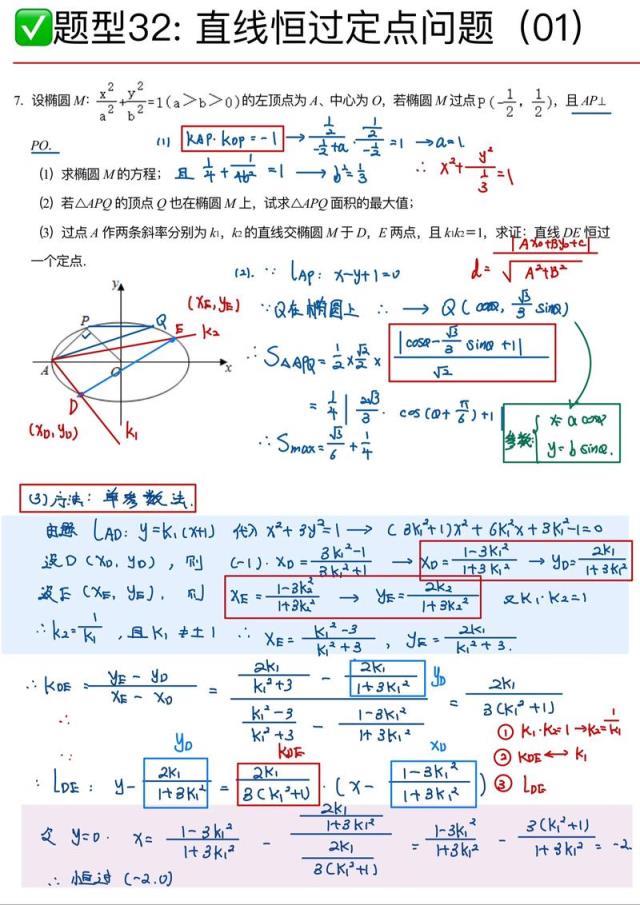
1. 平面几何图形：在解析几何中，圆锥曲线（椭圆、双曲线、抛物线）是核心，题目通常涉及求标准方程、探讨几何性质（焦点、离心率、渐近线等），以及处理直线与圆锥曲线的位置关系（相交、相切、相离）。

2. 立体几何图形：这部分主要考察空间中的点、线、面关系。

   • 三视图与直观图：要求能够根据三视图还原几何体的直观图,并计算其表面积和体积。
   • 空间位置关系证明：证明线线平行/垂直、线面平行/垂直、面面平行/垂直。
   • 空间角与距离计算：包括异面直线所成角、线面角、二面角，以及点到面的距离、异面直线间的距离等计算,常用方法有坐标法和几何法。

解析几何中的图形问题

解析几何的核心是用代数方法研究几何问题。

1. 直线与圆：考察直线的方程形式、圆的方程，以及直线与圆、圆与圆的位置关系判断。
2. 圆锥曲线的综合应用：常与向量、函数、不等式等知识结合，构成综合性大题，求动点的轨迹方程、探讨存在性问题、求解最值问题等。

向量相关的图形题

向量兼具代数与几何双重身份,是解决图形问题的有力工具。

1. 平面向量：利用向量可以轻松处理线段的长度、夹角问题，证明三点共线、两直线平行或垂直。
2. 空间向量：在立体几何中建立空间直角坐标系，利用向量法可以系统性地处理角度和距离的证明与计算,大大降低了思维难度。

概率统计中的图表题相对直观,但要求准确提取信息。

1. 统计图表分析：需要能够从频率分布直方图、茎叶图、散点图等图表中读取数据，计算平均数、方差等数字特征,或判断两个变量的相关性。
2. 正态分布曲线：理解正态分布曲线的特点，会利用对称性和3σ原则进行概率计算。

提升图形题解题能力的建议

必须重视基础知识，对每个基本图形的定义和性质了如指掌，养成画图的习惯，即使是抽象的代数问题，尝试画出草图往往能启发思路，加强归纳总结，将做过的图形题按类型分类，提炼通用的解题思想，例如在解析几何中设而不求、利用几何性质简化运算等。

图形题是数学能力的重要体现，通过系统学习和持续练习,完全可以掌握其解题规律。

本站通过AI自动登载优质内容，本文来源于互联网或者用户投稿，本站旨在传播优质文章，无商业用途。如不想在本站展示可联系删除