初中数学怎样判定相似三角形？

初中几何的基石与应用钥匙

在初中几何的殿堂里，相似三角形如同一个精巧的万用钥匙，解锁着众多图形问题的奥秘，理解并掌握它,能为后续的几何学习奠定坚实基础。

相似的本质：形状相同，大小可变

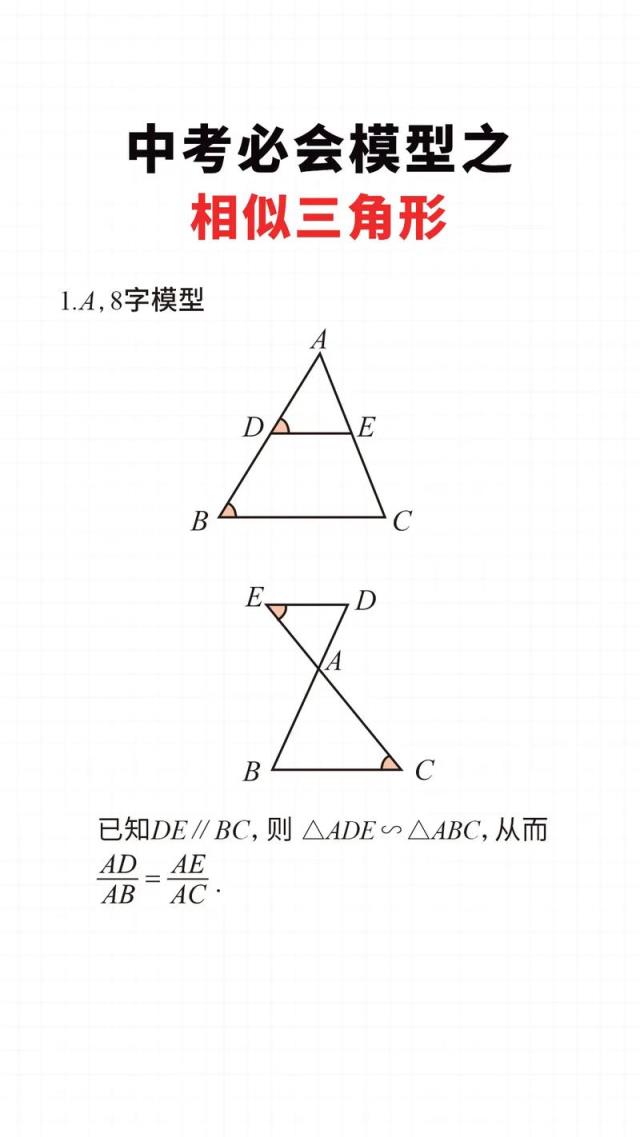
当两个三角形的对应角完全相等，且对应边成固定比例时，我们称这两个三角形相似，用符号“∽”表示，如△ABC ∽ △DEF，关键在于“形状一致”，大小可以不同,这就像同一张照片放大或缩小后的效果。

判定相似三角形的可靠方法

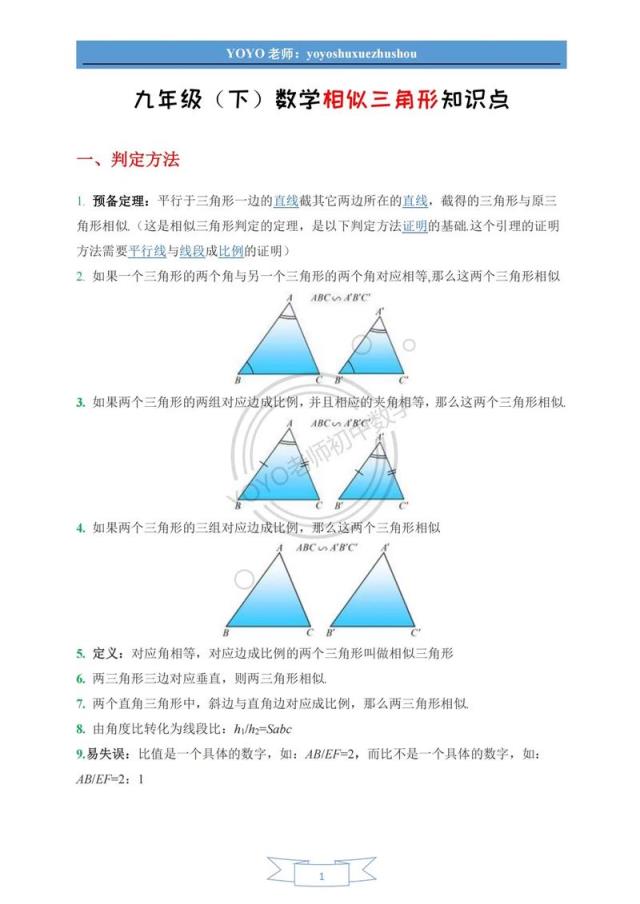
如何确认两个三角形相似？主要依据以下三条核心判定定理：

1. 两角对应相等（AA）：若两个三角形中有两组对应角分别相等，则它们必然相似,这是最常用也最直观的方法。

   • 实例：在△ABC和△DEF中，若∠A = ∠D 且 ∠B = ∠E，则△ABC ∽ △DEF。

2. 三边对应成比例（SSS）：若两个三角形的三组对应边的长度都成同一比例,则它们相似。

   • 实例：若在△ABC和△DEF中，AB/DE = BC/EF = AC/DF，则△ABC ∽ △DEF。

3. 两边成比例且夹角相等（SAS）：若两个三角形中有两组对应边成比例，并且这两组边所夹的角相等,则它们相似。

   • 实例：若在△ABC和△DEF中，AB/DE = AC/DF 且 ∠A = ∠D，则△ABC ∽ △DEF。

相似带来的核心性质

一旦确认两个三角形相似,一系列重要性质便随之而来：

• 对应角相等：这是相似定义的一部分。
• 对应边成比例：所有对应边的比值都等于同一个常数，称为相似比（k），即若△ABC ∽ △DEF，则 AB/DE = BC/EF = AC/DF = k。
• 周长比等于相似比：两个相似三角形的周长之比等于它们的相似比k。
• 面积比等于相似比的平方：两个相似三角形的面积之比等于相似比k的平方（k²）,这个性质在解决面积相关问题时非常强大。

相似三角形的实际应用价值

相似三角形绝非纸上谈兵,它在解决实际问题中大显身手：

• 测量不可达距离：这是最经典的应用，利用相似原理，可以轻松测量如河流宽度、高楼高度、旗杆长度等无法直接用尺子量取的距离。
  • 场景：站在操场上，如何测量教学楼高度？只需一根已知长度的直杆和一把尺子，竖直立起直杆，测量杆长、杆影长以及此时教学楼的影长，根据“同一时刻阳光下物体高度与其影长成比例”（本质是相似三角形）,即可列出比例式求出楼高。
• 解决复杂几何问题：在更复杂的平面几何图形（如含有平行线、相交线、嵌套图形等）中，相似三角形常是沟通不同部分关系的桥梁，用于证明线段比例、角度相等或计算未知量。
• 理解地图与模型比例尺：地图或模型上的图形与实际图形是相似的,比例尺体现的正是相似比。
• 物理光学成像：理解小孔成像、透镜成像等光学现象时,相似三角形的概念不可或缺。

个人观点在多年数学教学中，我深刻体会到相似三角形是初中几何承上启下的关键纽带，它不仅整合了全等、比例、角度等知识，更培养了学生观察图形结构、寻找比例关系的核心几何思维，真正掌握相似原理，意味着拥有了一把打开更广阔几何世界大门的钥匙，那些看似复杂的图形问题，往往在构造出恰当的相似三角形后便迎刃而解，建议学生在学习时，务必重视基本定理的理解和典型例题的分析，多动手画图尝试构造相似关系,这是提升解题能力的必经之路。